To, že hvězdy vidíme v minulosti, je představa založená na Einsteinově definici současnosti (označme si ji jako E-současnost), jak ji vyložil ve svém článku v roce 1905, kterým světlu světa představil svoji speciální teorii relativity (STR) se známou kontrakcí délek, dilatací času atd. Všechny tyto efekty se opírají o jeho definici současnosti.
Ta vychází z přirozené intuice, která například u blesku říká, že jeho zvuk k nám dorazí se zpožděním a blesk skutečně udeřil ve chvíli, kdy ho vidíme. Pro naše obvyklé rychlosti na Zemi totiž postačuje zjednodušení, považující rychlost světla prakticky za nekonečnou. Když rozsvítíme lampu ve tmě, zdá se nám přece, že je světlo všude okamžitě.
Odtud je naše intuitivní představa, že současnost je absolutní, tedy že skutečná podoba a poloha objektů je ta, která je teď, ať je těleso jakkoliv vzdálené, i když je to např. hvězda vzdálená třeba milión světelných let. Je to vlastně představa, že kdybychom se mohli pohybovat nekonečnou rychlostí a mohli bychom skočit ihned k dotyčné hvězdě, viděli bychom, jak v současnosti vypadá. Je to ale trochu problematická představa, pokud přejdeme ke STR.
V představě s bleskem hraje roli zvuku světlo, ale otázkou je, co hraje v STR metaforickou roli světla. Einstein žádnou konkrétní fyzikální interakci nenavrhl, a vypadá to tedy, že nevědomky uvažuje o imaginárním, nefyzikálním „pozorování“ nekonečnou rychlostí. To je podstata E-současnosti.
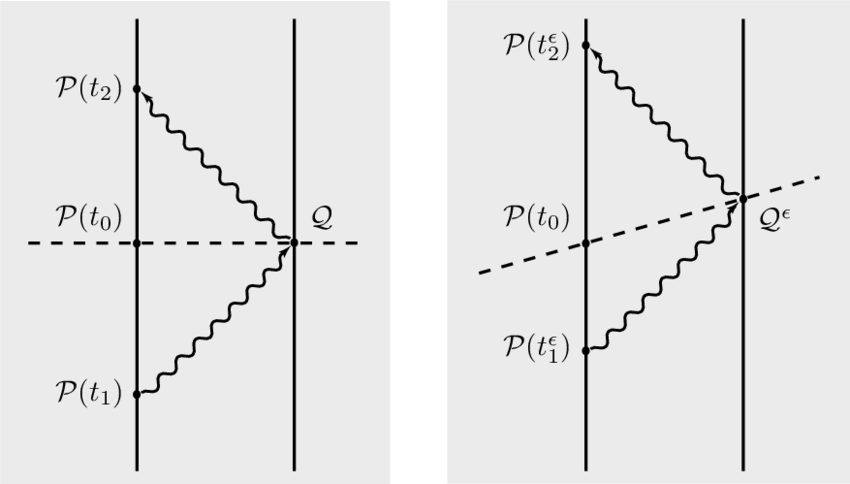
E-současnost totiž říká, že když vyšleme paprsek k tělesu, od kterého se odrazí a vrátí se k nám za čas t, pak okamžik odrazu paprsku od tělesa je současný s časem t/2 pozorovatele (viz obrázek výše, levý případ). Prostě logicky dělíme čas, po který paprsek letěl od pozorovatele a zpět, dvěma a získáme tak časové zpoždění paprsku pohybujícího se od tělesa k nám. Toto zpoždění Einstein odečetl a vytvořil tak abstraktní pozorování nekonečnou rychlostí. Tím jako by se v jistém slova smyslu částečně vrátil zpět k absolutnímu prostoru. Ten totiž měl jako limitní rychlost nekonečnou rychlost, kterou Einstein popřel ve prospěch rychlosti světla.
Otázkou je, jestli tím neopustil celou fyziku, neboť fyzika zkoumá reálné fyzikální jevy, a ne nějaké abstrakce. Einstein věděl, že každá fyzikální teorie musí stát na axiomech, které v danou chvíli není možné analyzovat, ale jsou nicméně nutné ke stavbě dané teorie. Takové axiomy jsou prakticky vždy zjednodušením, které bude překonáno. Otázkou je, jestli takový axiom Einstein udělal fyzikálně korektně.
Když se pokusíme nevypadnout z fyziky a ono pozorování budeme chtít „materializovat“, budeme předpokládat, že je realizováno nějakou nadsvětelnou interakcí, budeme mít zase problém se základním postulátem speciální relativity, limitní rychlostí světla, který by žádná interakce neměla překonat. Můžeme sice argumentovat tím, že takovýto okamžitý skok například ke vzdálené hvězdě je jen představa, fiktivní pohyb, ale pak je otázkou, jestli už nejsme ve spiritistickém kroužku. Einstein výrazně kritizoval strašidelné kvantové působení na dálku, tedy kvantovou provázanost, v čemž se evidentně spletl, ale tato strašidelná současnost na dálku mu evidentně nevadila.
Máme jen dvě možnosti. První je uvažovat, že existuje nějaká skutečná fyzikální interakce, která je prakticky nekonečně rychlá. Jediný dnes známý kandidát je kvantová provázanost, která údajně ihned spojuje dvě, třeba světelný rok vzdálené částice. V každém případě je tato úvaha o provázanosti pouze velmi hypotetická. Nicméně, kdyby byla pravdivá, pak by i speciální teorie zřejmě byla svým způsobem kvantovým jevem.
Druhou možností je pokorně se spolehnout na „pomalé“ světlo a současnost definovat tak, že současné je to, co vidíme současně. Tedy, že se rozhlédneme po hvězdné obloze a prohlásíme, že všechny hvězdy vidíme v současnosti, ne v minulosti. Tahle zdánlivě nesmyslná představa je překvapivě obsažena i ve zmíněném Einsteinově článku z roku 1905. Konkrétně Albert píše: „Mohli bychom se zajisté spokojit s takovým ohodnocením událostí v čase, že pozorovatel nacházející se i s hodinami v počátku souřadnic, přiřadí událostem tu polohu hodinových ručiček, při níž k němu dospěje prázdným prostorem světelné znamení.“
Tuto současnost, označme si ji jako F-současnost (fenomenologickou, jevovou současnost), vyřazuje Einstein jako nepraktickou, nikoliv však fyzikálně nekorektní. Má tedy šanci na úspěch. Proveďme analýzu předností a nedostatků obou definic současnosti.
Daň za „nefyzikální“ Einsteinovu současnost je, že jsou efekty teorie relativity fyzikálně nepozorovatelné, jak ve svých článcích upozornili Lampa (1924), Terrell a Penrose (oba 1959). Výmluvný už je název Terrellova článku: „Invisibility of the Lorentz Contraction“. Obsahově podobný je i článek Rogera Penrose. Tedy efekty Einsteinovy speciální teorie relativity jsou tak nějak neviditelné a nemůžeme se o nich přesvědčit přímo, ale můžeme je jen vypočítat. Přesvědčujeme se tak o nich pouze prakticky kontaktně, při velmi lokálních měřeních (například obíhání částic v urychlovačích), ale protože tam se E-současnost a F-současnost shodují, nepomůže nám to příliš při rozhodování, která z těchto současností je skutečně správná.
Když vyměníme E-současnost za F-současnost, dostaneme odlišnou podobu Einsteinovy teorie, F-STR, a ta bude vypadat výrazně jinak, než jsme zvyklí. Tělesa se budou kroutit, nejen zkracovat, ale i natahovat (při rychlosti tělesa rovnou rychlosti světla směrem k pozorovateli se bude např. jevit těleso jako „nekonečně“ dlouhé), a různě deformovat tzv. Terrellovým efektem, viz obrázek výše. Nicméně vše bude nejen fyzikální, ale také nikoliv mimo teorii relativity, jako E-současnost. Řekněme jasně, že F-STR je fyzikálně a logicky zcela korektní a konzistentní, je fyziky chápána jako jakási vizuální podoba E-STR a bylo o ní napsáno mnoho korektních vědeckých článků.
Jsou tedy vlastně dvě vědecky uznávané podoby STR, ale o E-STR se má za to, že je to ta pravá, kdežto F-STR je jen její jevová podoba, takže něco zdánlivého, asi jako lupou deformovaná podoba objektů. To by určitě platilo, kdyby byla E-STR spolehlivě pravdivá.
V každém případě nikdo nepochybuje, že např. zmenšování vizuálního obrazu člověka, který se vzdaluje, je vědecký fakt a pro vizuální velikost existuje exaktní vzorec, nicméně se tato velikost pokládá pouze za zdánlivou. Všimněme si mimochodem, že skutečná velikost se zde určuje kontaktním měřením, což je stejné jako v STR. Soumístné údaje eliminují zkreslující jevy a jsou proto považovány za absolutní, absolutně spolehlivé, tedy skutečné. Není-li ale těleso soumístné s pozorovatelem (což ostatně nikdy není úplně už kvůli rozměrům pozorovatele a tělesa), nenahlížíme na skutečnost přímo, ale dopočítáváme si ji či představujeme na základě předchozí zkušenosti.
Takovéto „dopočítávání“ skutečnosti, vlastně její abstraktní modelování, může ale obsahovat systematické chyby modelu. Ale jevy, jako třeba F-STR, mají tu výhodu, že jsou vnímány bezprostředně(ji), a to znamená jejich větší spolehlivost, jistotu vyhnutí se systematickým chybám modelu. Na to vsadila třeba Kodaňská interpretace kvantové mechaniky a Schrödingerova rovnice, která je spolehlivým jevovým popisem s úžasnou přesností výpočtu, ale pravou podstatu kvantové mechaniky zřejmě míjí. Nahlédnutí podstaty (E-STR) za jevy (F-STR) má zase obecnější platnost, větší solidnost a menší proměnlivost oproti jevům.
Osobně se mi více líbí Einsteinův přístup hledání skutečné podstaty (která je nicméně ale jen hlubším jevem), ale je potřeba poukázat na jeho možné chyby. Odmítněme námitku, že E-současnost porušuje postulát limitní rychlosti světla tím, že pochopíme, že toto „abstraktní“ pozorování je také fyzikální, ale mimo STR, proto její postulát nemusí respektovat. Zůstali jsme ve fyzice, nejsme v nějaké abstraktní sofistice, konzistentnost teorie relativity je zachráněna, ale jako výchozí postulát se neukazuje pouze princip relativity nebo limitní rychlost světla, ale také definice současnosti. To nás ale logicky vytlačuje mimo náš 3D prostor, neboť v našem prostoru se zřejmě nelze pohybovat nadsvětelně, tedy použít E-současnost. Stačí si dosadit nadsvětelnou rychlost do vzorců E-STR, abychom to zjistili. Ale právě v tomto 3D prostoru, tedy oblasti, kde se šíří světlo, Einstein definuje svou E-současnost. Není to chyba? Nemá být současnost definována ve 4D „prostoročasu“?
Kdyby tuto chybičku udělal, mělo by to mít nějaké špatné důsledky. A ty jsou tady. Jedním z těchto problémů může být konvencionalita současnosti, jak ji vykládá Reichenbach a Grünbaum. Einstein automaticky předpokládal, že rychlost světla od pozorovatele k tělesu bude stejná jako rychlost zpět. To samozřejmě logicky dobře funguje, uvažujeme-li newtonovské médium v klidu. Jenže STR není klasická fyzika a s klidem se to má dost podivně. V klidu je jaksi jak pozorovatel, tak vzdalující se těleso, od kterého se paprsek odráží, vlastně jako všechny inerciální soustavy. I těleso, tedy každá inerciální soustava, může vyslat synchronizační paprsek (k pozorovateli). Kdyby se tyto rychlosti v protikladných směrech (od pozorovatele a k pozorovateli) lišily, byla by STR i tak konzistentní, i když poněkud jiná, nicméně ekvivalentní. Platila by Reichenbachova definice současnosti, jak ji zobrazuje možnost vpravo na obrázku č. 2. Neexistuje žádné fyzikální měření, které by ověřovalo, že E-současnost je ta pravá. Námitka konvencionality ale není až tak silná, neboť dokonce i Reichenbach nakonec usoudil, že E-současnost je nejlepší volba.
Ale hlavní problém E-STR je paradox Andromedy neboli Rietdijkův–Putnamův paradox. Ten vysvětluje, že když budou v jednom okamžiku na jednom místě dva pozorovatelé třeba jedoucí na kole proti sobě, jeden směrem ke galaxii Andromedy a druhý od ní, a předají si informaci o tom, co je na Andromedě v tuto chvíli za čas, bude se jejich E-STR údaj lišit o hodně dní. A když bychom takhle složili hodně v daný okamžik soumístných pozorovatelů pohybujících se různými rychlostmi, „viděli“ bychom „celou“ minulost i budoucnost Andromedy.
Problém E-STR ale je, že bychom právě nic takového neviděli, neboť neexistuje žádný fyzikální způsob, jak předat takovou informaci o současnosti z Andromedy na Zemi. Všichni pozorovatelé by museli trpělivě počkat několik miliónů let, než k nim dorazí světelné paprsky obsahující informaci, jaký že je čas a co se děje na Andromedě. E-současnost jako by tady vůbec (fyzikálně) neexistovala. Můžeme uvážit, že přece když něco nevidíme, neznamená to, že to neexistuje, jenže o existenci se ve fyzice musíme vždy přesvědčit pozorováním či experimentem, a právě to je tady neproveditelné. Buď je to jen se současnými znalostmi neproveditelné, a pak musí jít dál, za E-STR, hledat možnost nadsvětelného fyzikálního pozorování, nebo je to v principu neproveditelné.
Kouzelné u paradoxu Andromedy je, že když přejdeme k F-současnosti a tedy F-STR, paradox okamžitě zmizí. Všichni, libovolnou rychlostí se pohybující soumístní pozorovatelé si musejí počkat na světelný paprsek, když se setkají v jednom bodě, a ten bude stejný pro všechny a ponese zcela stejnou informaci o čase. Fyzikálně tedy nelze vidět ani současnost ani budoucnost, jen F-přítomnost.

