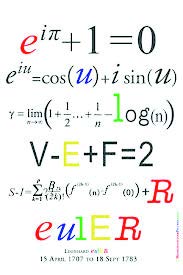Existuje mnoho různých zdrojů krásy. Krásná tvář, malebná krajina nebo velkolepá symfonie jsou příklady krásy, kterou vnímáme svými smysly. Existují ale i jiné, vysoce intelektuální zdroje krásy. Matematici často popisují matematické vzorce emotivními výrazy a požitek z krásy matematiky často přirovnávají k zážitkům z největších uměleckých děl.
Existuje mnoho různých zdrojů krásy. Krásná tvář, malebná krajina nebo velkolepá symfonie jsou příklady krásy, kterou vnímáme svými smysly. Existují ale i jiné, vysoce intelektuální zdroje krásy. Matematici často popisují matematické vzorce emotivními výrazy a požitek z krásy matematiky často přirovnávají k zážitkům z největších uměleckých děl.
Nová studie publikovaná v časopisu Frontiers in Human Neuroscience (Hranice lidské neurovědy) popisuje, jak výzkumníci ukazovali patnácti matematikům vzorce, které předtím zhodnotili jako krásné, neutrální nebo ošklivé. Pomocí magnetické rezonance přitom zkoumali jejich mozkovou aktivitu. Výsledky ukázaly, že krása matematiky vzbuzuje aktivitu ve stejné části mozku, konkrétně v orbito-frontálním kortexu, jako krása uměleckých děl nebo hudby.
Profesor Semir Zeki z neurobiologické laboratoře na UCL, který tento výzkum vedl, řekl: „Mnohým z nás se matematické vzorce zdají suché a nepřístupné, ale pro matematika může být rovnice ztělesněním krásy. Krása vzorce může spočívat v jeho jednoduchosti, symetrii, eleganci nebo v tom, že vyjadřuje neměnnou exaktní pravdu. Již Platon matematiku považoval za nejvyšší vrchol krásy. Proto je zajímavé zkoumat, zda krása matematiky, která je tak intelektuální a abstraktní, vyvolává aktivitu ve stejné části mozku jako krása vnímaná z emocionálních a vjemových zdrojů.“
Zkoumaní matematici dostali během studie 60 matematických vzorců, které si měli v klidu prohlédnout a ohodnotit na stupnici od -5 (ošklivý) do 5 (krásný) podle toho, jak se jim vzorec líbí. O dva týdny později byli požádáni, aby vzorce ohodnotili znovu. Jejich mozek byl přitom zkoumán pomocí magnetické rezonance.
Vzorce nejčastěji hodnocené jako krásné (a to jak před, tak během skenování) byly Eulerova rovnost, Pythagorova věta a Cauchyho-Riemannovy rovnice. Eulerova rovnost (eiŔ + 1 = 0) spojuje pět základních matematických konstant pomocí tří základních aritmetických operací, z nichž každá se ve větě vyskytuje právě jednou. Krása této rovnice bývá přirovnávána k monologu v Hamletovi. Jako nejošklivější ohodnotili matematici Srinivasa Ramanujanovy nekonečné řady a Riemannovu funkci zeta.
Profesor Zeki dodal: „Zjistili jsme, že stejně jako u vnímání vizuální krásy nebo hudebních zážitků činnost mozku úzce souvisí s tím, za jak intenzivní své zážitky lidé považují – dokonce i v tomto případě, kde je zdroj krásy velmi abstraktní. Tato studie nabízí odpověď na důležitou otázku z oboru estetiky. Na otázku, o které se již dlouho diskutuje – a to, zda lze estetické vjemy kvantifikovat.“