V příjemném prostředí restaurace Austria na Praze 5 na setkání Business Clubu 10.3.2009 proběhla zajímavá beseda na téma Aplikace teorie her v ekonomice a politice. Účastníky přivítal Vladimír Souček a poté předal slovo Václavu Janouškovi, který přednesl obsáhlý úvodní výklad.
Průběh akce byl pro mě několikanásobným příjemným překvapením. Již první část vystoupení věnovaná zajímavým aplikacím a interpretacím typu her, které se nazývají „vězňovo dilema“, obsahovala řadu původních postřehů a interpretací. Ve druhé části byly zmíněny některé myšlenky z knihy o teorii her a redistribučních systémech, která mi nedávno vyšla. [1] Potěšilo mě, že se o ní ví i v tomto prostředí a že inspirovala část diskuse. Zejména jsem pak ocenil, že již v průběhu večera dvojice přítomných dokázala vyřešit poměrně náročný problém dělení dědictví mezi pět bratrů [2] a další z účastníků – Jiří Volf – mi řešení poslal hned další den. Přesvědčil jsem se, že mensané skutečně umí myslet.
Způsob logického uvažování, který jsem měl možnost sledovat již na besedě, přesné odhalení velmi jemných a skrytých předpokladů, na kterých stojí řešení, tak jak je obsahoval mail jednoho z účastníků zaslaný hned druhého dne, mi vnuklo nápad: Dokážou se takto mensané vyrovnat s některými obdobnými otevřenými problémy, s nimiž si láme hlavu náš tým řešící problematiku modelování procesu vyjednávání v redistribučních systémech?
Problém dělení dědictví mezi pět racionálních, ale zlých bratrů je typický příklad z oblasti teorie her, kdy dochází k distribuci prostředků na základě vytváření koalic. Teorie redistribučních systémů se zabývá obdobnou problematikou, ovšem vztaženou k praxi. Pokud by měl někdo zájem dozvědět se o ní něco více, mohu mu doporučit podkladové materiály z archivu našeho pravidelného teoretického semináře. [3]
Pokusím se stručně sdělit, o jaké otevřené problémy teorie redistribučních systémů jde, včetněkontextu jejich vzniku a významu řešení. Především je nutné zdůraznit, že modelování různých typů vyjednávání není samoúčelné. Hledáme prostřednictvím něj „zajímavé“ strategie vyjednávání. Ovšem které strategie vyjednávání jsou zajímavé? S trochou nadsázky lze říci, že ty, které jsou „vytaženy z Platónovy říše idejí“. Poznají se podle toho, že se těžko hledají a když se najdou, zjistí se, že jsou tak samozřejmé, že jinak to ani nemůže být… Kromě toho má nalezení takové „platónské“ strategie zpravidla značný význam jak pro další rozvoj teorie, tak i při praktických aplikacích.
Teorie her se zabývá situacemi, kdy je výsledná situace určena nejen naší volbou, ale i volbou někoho jiného, případně několika dalších subjektů. Řešení konkrétních úloh předpokládá, že známe hráče, strategie, kterými disponují, a výplatní matici, tj. to, kolik kdo dostane, pokud jednotliví hráči uplatní některou ze svých strategií. [4] Hry rozlišujeme podle několika kritérií. Jedním z nich je počet hráčů. Poměrně dobře jsou matematicky popsány hry se dvěma hráči. Hry s více hráči jsou mnohem složitější, zejména pokud uvažujeme, že mohou vznikat koalice a docházet k vyjednávání mezi hráči. Jedním z případů je i teorie redistribučních systémů, která vychází ze dvou předpokladů: 1. čím větší je odchylka odměn hráčů od jejich výkonnosti, tím více poklesne výkon systému; 2. příčinou této odchylky je vznik koalic. Model elementárního redistribučního systému je koncipován tak, aby postihl to nejdůležitější a současně nejjednodušší, s čím se v dané oblasti setkáváme. V logice věci má tři hráče (A, B, C), každý z nich má stejný vliv na daný systém, kteříkoliv dva hráči mohou vytvořit koalici, výkonnost hráčů je oceněna malými přirozenými čísly (např. 6:4:2). Výplaty hráčů pak můžeme zobrazit ve trojrozměrném prostoru, kdy každé ose souřadnic odpovídá výplata některého z hráčů. Vliv snížení efektivnosti systému v důsledku odchylky výplat od výkonnosti hráčů můžeme vyjádřit redistribuční rovnicí, např. x + y + z = 12 – ·.R(x – 6, y – 4, z – 2), kde x + y + z je součet skutečných výplat jednotlivých hráčů; 12 je maximální odměna, která by mohla být rozdělena, pokud by výkon redistribučního systému byl maximální, což znamená, že by nedocházelo k redistribuci, rozdělení výplat by proběhlo podle výkonnosti; · je koeficient snížení výkonnosti; R(x – 6, y – 4, z – 2) je funkce vzdálenosti rozdělení skutečných výplat od výplat podle výkonnosti hráčů (v našem přístupu ji modelujeme jako prostorovou vzdálenost, tj. odmocninu ze součtu čtverců).
Struktura všech možných (tedy i nezajímavých) strategií v redistribučních systémech je složitá. Každý hráč má totiž následující možnosti: 1. dát návrh na rozdělení výplat jednomu hráči, druhému hráči, oběma hráčům současně; 2. čekat až jiný hráč dá návrh a reagovat na něj – přijmout, odmítnout; 3. čekat až dá druhý návrh třetí hráč a reagovat na obě nabídky. Přitom každý návrh na rozdělení podle redistribuční rovnice (tj. na redistribuční ploše) je konkretizací obecné strategie, tj. množina strategií je vícerozměrná s mohutností kontinua (každý hráč má nekonečně mnoho, dokonce nespočetně mnoho strategií).
První nalezená skutečně zajímavá strategie platónského typu umožnila, aby model vyjednávání začal chodit na počítači. Současně ukázala, že vyjednávání za podmínek orientace na tuto strategii konverguje k dosažení tří nestabilních rovnováh, v nichž vždy dva hráči diskriminují třetího. Nazvali jsme ji elementárním typem strategie vyjednávání. Lze ji ve stručnosti popsat takto: Předpokladem je, že každý hráč zná všechny kombinace výplat. Ke změně dojde, pokud si dva hráči zvýší výplatu. Jednání iniciuje vždy hráč, který je diskriminován (tj. je vně koalice). Tento hráč zná, jaké jsou výplaty ostatních dvou hráčů, a na základě toho dovede určit i to, jakou výplatu by měl v koalici s každým z hráčů stávající koalice, pokud by se jeho výplata (tj. výplata příslušného hráče, který tvoří stávající koalici) nezměnila. Vytvoření nové koalice nabídne tomu hráči, s nímž by měl větší výplatu, pokud by velikost výplaty hráče, kterému vytvoření koalice nabízí, zůstala zachována. Sobě navrhne výplatu, která se rovná procentuálně stanovému podílu (např. průměru, tj. 50 %) z rozdílu mezi největší a nejmenší možnou výplatou, kterou může v nové koalici dosáhnout. Od své výplaty odvodí velikost výplaty toho hráče, kterému vytvoření koalice nabídne, a ten tuto nabídku přijme. Diskriminovaným se pak stává druhý z hráčů předcházející koalice, který nyní podle stejných pravidel nabídne vytvoření nové koalice.
Odhalení rovnováh, ke kterým systém konverguje v případě vyjednávání na bázi elementární strategie, pak umožnilo zjistit, jak se systém chová, pokud na něj působí různé vnější vlivy (konkurence, možnost meziorganizační migrace, možnost nepředvídatelné změny výkonností hráčů apod.), tj. kam se posouvají tyto rovnováhy v případě, že je systém těmto vlivům vystaven. Z toho rovněž vyplynulo, čím lze argumentovat (případně doplnit argumentaci), pokud chceme vyjednat výhodnější podmínky.
Především však již první jednoduchý systém vyjednávání založený na strategiích platónského typu umožnil odhalení mimořádně významné skutečnosti. Totiž toho, že vnější vlivy lze rozlišit na kompenzované (kompenzovatelné) a nekompenzované (nekompenzovatelné). Pokud se podaří zablokovat určitý typ argumentace, pak nekompenzované vnější vlivy predeterminují typ koalice, který vznikne. To, co blokuje určitý typ argumentace se pak může replikovat („rozmnožovat“) v komunikačním prostoru a vést k predeterminování rovnováhy ve velkém množství reálných redistribučních systémů, následně pak vznikukřížových koalic mezi těmito systémy i od nich se odvíjejících sociálních sítí. Blokující replikátory, které tuto roli plní, jsou přitom v komunikačním prostoru vystaveny konkurenci („boji o přežití“), což vede k jejich zdokonalování, resp. vývoji. Čím větší je intenzita komunikace v příslušném komunikačním prostoru, tím silnější podněty pro vývoj replikátorů uvedeného typu na bázi přirozeného výběru vznikají. [5]
Existují však i jiné, dosud přesně nepopsané, neformalizované a tudíž i nepřenesené do podoby, která by umožnila jejich simulaci na počítači, typy vyjednávacích strategií, které mají významné důsledky. V současné době např. intenzivně hledáme strategii, která by umožnila „pozvednutí“ vývoje v redistribučním systému ze situací, kdy se vytvářejí diskriminující koalice, k situaci, která je pro všechny hráče „nejvýhodnější“. Musíme ovšem upřesnit i to, co znamená „nejvýhodnější“ v tomto kontextu. Jedná se totiž o situaci, která má rysy jak paretovské, tak i nashovské rovnováhy. [6]
Model elementárního vyjednávání v redistribučním systému ukazuje následující: 1 střídají se případy, kdy každý hráč je ve vítězné koalici a kdy je mimo ni a je tedy diskriminován; 2. střídají situace, kdy každý hráč má ve vítězné koalici o něco více a kdy o něco méně.
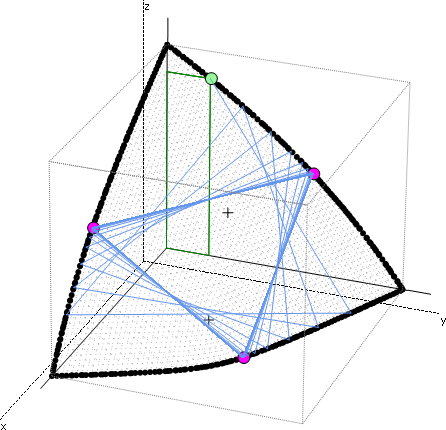
Počítačové zobrazení procesu vyjednávání vypadá takto: Souřadnice zde představují výplaty hráč. Projekce redistribuční plochy je ohraničena silnými černými křivkami. Ty současně představují body, kdy má jeden z hráčů nejnižší možnou výplatu. V daném případě je výchozí, tj. první dojednaná situace označena zeleným bodem. Slabé modré linii ukazují další kroky vyjednávání, které postupně konverguji ke třem fialovým bodům – příslušným nestabilním diskriminačním rovnováhám.
Jeden z účastníků (a některý bude první, pro ostatní to v tu chvíli ještě nebude platit) zjistí následující: Pokud vyplatí každému z druhých hráčů průměr dvojnásobku větší výplaty a nejmenší výplaty, tj. více než mají průměrně, jeho vlastní výplata bude vyšší než jeho průměrná výplata. Tj. může navrhnout paretovské zlepšení, na kterém vydělá on sám nejvíce.
Matematicky vypadá návrh každému ze dvou ostatních hráčů takto: 1/3 krát (2 krát vyšší poslední výplata ve vítězné koalici plus 1) oběma ostatním hráčům a sobě to, co vyjde jako řešení redistribuční rovnice.
Odsud vyplývají otázky: 1. Jak dojde k tomu, že se hra „pozvedne“ z vytváření plně diskriminujících koalic (v nichž jeden hráč má vždy nejmenší možnou výplatu) k vytváření koalic, kdy i diskriminovaný hráč dostane výplatu vyšší (a v procesu vyjednávání rostoucí), resp. kdy přestává být diskriminován? 2. Kdy a jak konverguje proces vyjednávání v tomto případě k rovnováze, ve které není nikdo diskriminován?
Za těmito otázkami se skrývá mnohem více, než by se na první pohled zdálo – jde totiž o přechod od konfrontace ke kooperaci zúčastněných hráčů; existuje určitá naděje, že identifikování a popis příslušné strategie vyjednávání odhalí to, co je přítomno v každém přechodu od konfrontace k rozumnějšímu řešení problémů.
Lze namítnout, že zadání problému (hledání konvergenční strategie) není zcela přesně definováno. Ale to je standardní badatelská situace. Zformulovat úplně přesné zadání je skoro totéž jako již dát hotové řešení. Vyjasňování předpokladů zpravidla probíhá současně s upřesňováním zadání.
O autorovi
Radim Valenčík (1953) působí na Vysoké škole finanční a správní jako vedoucí katedry ekonomie a mezinárodních vztahů. Rediguje internetový časopis Marathon věnovaný společenskovědní problematice. Je rovněž členem Institutu pro sociální a ekonomické analýzy.
Poznámky
[1] Valenčík, R., Teorie her a redistribuční systémy, Praha, VŠFS EUPRESS 2008. Podrobné informace o knize včetně většího výňatku a recenzí jsou na http://www.palmknihy.cz/
[2] Lze nalézt na www.scienceworld.cz/sw.nsf/ID/80E893693576F0BDC12571140063B8BA?OpenDocument
[3] Jsou ke stažení na www.vsfs.cz/?id=1046
[4] Velké množství materiálů k teorii her lze nalézt prostřednictvím Google. Doporučuji zejména http://euler.fd.cvut.cz/predmety/teorie_her/ , kde jsou plné texty přednášek RNDr. Magdalenay Hykšové, Ph.D. z Ústavu aplikované matematiky Fakulty dopravní ČVUT. V tištěné podobě jsou velmi dobrá skripta nedávno zesnulého Prof. RNDr. Miroslava Maňase, Dr.Sc. Teorie her a konflikty zájmů, která vyšla na VŠE v roce 2002.
[5] Tím se náš výzkum dostal velmi blízko tomu, co se nazývá teorií memů. Zájemcům o tuto oblast poznání, které někteří nepřiznávají status vědy, lze odkázat např. na knihu Susane Blackmoreové Teorie memů, která vyšla v roce 2001 v nakladatelství Portál.
[6] Paretovská rovnováha je situace, kdy nejsou možná paretovská zlepšení, tj. když si nikdo nemůže polepšit, aniž by si někdo jiný nepohoršil. Nashovská rovnováha je situace, kdy každý ze subjektů systému (hráčů) realizuje jako svou strategii tu, která počítá s nejhorší možnou reakcí protihráčů usilujících o maximalizaci svého užitku.